Canvas Draw Circle at Radiu
HTML5 Canvass arcs tutorial
Drawing arcs
You can draw arcs on canvas using the arc() method. Before going details on drawing arcs, hither's a brief overview on radian and angle :
The radian is the standard unit of angular measure, used in many areas of mathematics. An bending's measurement in radians is numerically equal to the length of a corresponding arc of a unit circle, so 1 radian is just nether 57.3 degrees (when the arc length is equal to the radius). The radian is represented by the symbol rad An alternative symbol is the superscript letter c. So for case, a value of ane.3 radians could be written as i.three rad or one.3c. See the following diagram :

Use the following formula to convert degrees to radians:
var radians = degrees * Math.PI/180
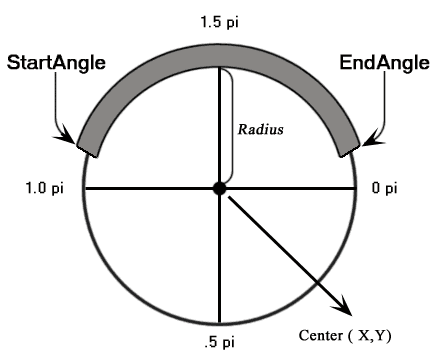
arc Method: arc(x, y, radius, startAngle, endAngle, direction)
| Parameters | Type | Clarification |
|---|---|---|
| x | number | The x-coordinate (in pixels), for the centre point of the arc in relation to the upper-left corner of the canvas rectangle. |
| y | number | The y-coordinate ( in pixels), for the center point of the arc in relation to the upper-left corner of the canvas rectangle. |
| radius | number | The radius or altitude from the betoken (x,y) that the arc's path follows. |
| startAngle | number | The starting bending, in radians, clockwise, with 0 corresponding to the 3:00 o'clock position on the right of the circle. |
| endAngle | number | The ending angle, in radians. |
| management | bool | true : The arc is drawn in a counterclockwise management from showtime to terminate. faux : The arc is drawn in a clockwise direction from start to end. |
Example : HTML5 Canvas arc using arc() method
The following web document creates a uncomplicated arc.
Output :

Code:
<!DOCTYPE html> <html> <head> <championship>Sample arcs example</championship></head> <torso> <sail id="demoCanvas" width="340" tiptop="340"> canvas</canvass> <script> var canvas = document.getElementById('demoCanvas'); var ctx = canvas.getContext('second'); var x = 90; var y = 100; var radius = 75; var startAngle = 1.ane * Math.PI; var endAngle = i.nine * Math.PI; var counterClockwise = false; ctx.beginPath(); ctx.arc(x, y, radius, startAngle, endAngle, counterClockwise); ctx.lineWidth = 10; // line color ctx.strokeStyle = 'green'; ctx.stroke(); </script> </body> </html> Example : HTML5 Canvas miscellaneous arcs
The following spider web document creates diverse types of arcs.
Output :
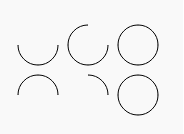
Lawmaking :
<!DOCTYPE html> <html> <head> <title>Sample arcs example</championship> <script type="text/javascript"> office misc_curves() { var canvas = document.getElementById("Mycanvas"); if (canvas.getContext) { var context = canvas.getContext("2d"); for (var i = 0; i < 2; i++) // Pace through two rows. { // Step through three versions. for (var j = 0; j < 3; j++) { context.beginPath(); // The 10-coordinate. var x = 35 + j * 50; // The y-coordinate. var y = 35 + i * 50; // The arc radius. var radius = twenty; // The starting point on the circle. var startAngle = 0; //end point on the circumvolve. var endAngle = Math.PI + (Math.PI * j) / two; // The management of drawing. var anticlockwise = i % ii === 0 ? simulated : true; // Create the arc path. context.arc(x, y, radius, startAngle, endAngle, anticlockwise); // Testify the arcs context.stroke(); } } } } </script> </head> <body onload="misc_curves();"> <sail id="Mycanvas" width="340" height="340"> sail</canvas> </body> </html> Drawing Circles
An arc is a role of a circle. To draw a circle, depict an arc with a starting bending of 0 and ending bending of two x Pi. Here is an example :
Output :

Code :
<!DOCTYPE html> <html> <head> <title>Sample arcs example</title></head> <body> <sail id="demoCanvas" width="340" height="340"> canvas</canvas> <script> var sail = document.getElementById('demoCanvas'); var ctx = canvass.getContext('2nd'); var x = xc; var y = 100; var radius = 75; var startAngle = 0; var endAngle = two * Math.PI; var counterClockwise = false; ctx.beginPath(); ctx.arc(10, y, radius, startAngle, endAngle, counterClockwise); ctx.lineWidth = 10; // line color ctx.strokeStyle = 'blue'; ctx.stroke(); </script> </body> </html> arcTo Method: arcTo(x1, y1, x2, y2, radius)
The arcTo() method creates an arc of radius between two tangents. The first tangent is defined past an imaginary line that is drawn through the final point in a path and the point (x1, y1). The second tangent is defined past an imaginary line that is drawn through the betoken (x1, y1) and the point (x2, y2).
Syntax :
arcTo(x1, y1, x2, y2, radius);
| Parameters | Type | Clarification |
|---|---|---|
| x1 | number | The x-coordinate for the kickoff tangent that intersects with the current path betoken. |
| y1 | number | The y-coordinate for the first tangent that intersects with the electric current signal. |
| x2 | number | The x-coordinate for the second tangent that intersects with the x1 and y1 points. |
| y2 | number | The y-coordinate for the second tangent that intersects with the x1 and y1 points. |
| radius | number | The radius of the arc to create. |
Instance : HTML5 Sail arcTo() method
The post-obit web document creates a rounded corner betwixt a horizontal and a vertical line.
Output :
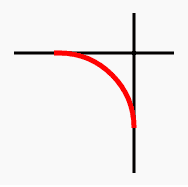
Code :
<!DOCTYPE html> <html> <head> <championship>Sample arcs instance</title></head> <trunk> <sheet id="myCanvas" width="300" height="600"></canvas> <script> var sheet = document.getElementById("myCanvas"); if (canvas.getContext) { var ctx = sheet.getContext("2d"); // Draw the imaginary tangents in blue. ctx.beginPath(); ctx.lineWidth = "three"; ctx.strokeStyle = "black"; ctx.moveTo(80, 100); ctx.lineTo(240, 100); ctx.moveTo(200, 60); ctx.lineTo(200, 220); ctx.stroke(); // Draw it. // Create two lines that have a connecting arc that could be used equally a starting time to a rounded rectangle. ctx.beginPath(); ctx.strokeStyle = "cerise"; ctx.lineWidth = "5"; ctx.moveTo(120, 100); // Create a starting indicate. ctx.arcTo(200, 100, 200, 220, 75); // Create an arc. ctx.stroke(); } </script> </torso> </html> HTML5 Canvas : Drawing Bezier Curves
Bezier curves are used in computer graphics to produce curves which announced reasonably smooth at all scales. Originally adult by Pierre Bézier in the 1970'southward for CAD/CAM operations. In vector graphics, Bézier curves are used to model smooth curves that can be scaled indefinitely. "Paths," every bit they are commonly referred to in image manipulation programs, are combinations of linked Bézier curves. Bézier curves are also used in animation as a tool to control motion
You tin draw bezier curves in the aforementioned manner every bit yous draw lines, just instead of using the lineTo() method, you employ either the bezierCurveTo() method or quadraticCurveTo() method. bezierCurveTo() method connects the endpoints with a cubic bezier curve using a specified pair of control points and the quadraticCurveTo() method connects the endpoints with a quadratic bezier curve using a single specified control signal.
bezierCurveTo() method
A cubic Bézier curve must include three points. The commencement 2 points (cp1x,cp1y) and (cp2x, cp2y) are control points that are used in the cubic Bézier calculation and the last point (x,y) is the catastrophe point for the bend.
Syntax:
bezierCurveTo(cp1x, cp1y, cp2x, cp2y, x, y)
| Parameters | Type | Description |
|---|---|---|
| cp1x | number | The 10-coordinate of the first Bézier command betoken. |
| cp1y | number | The y-coordinate of the first Bézier command point. |
| cp2x | number | The x-coordinate of the 2nd Bézier control point. |
| cp2y | number | The y-coordinate of the 2nd Bézier control bespeak. |
| ten | number | The x-coordinate of the signal to add to the current path. |
| y | number | The y-coordinate of the indicate to add to the electric current path. |
Note : The first point on the curve is the concluding signal in the existing electric current subpath. If a path does not exist, use the beginPath and moveTo methods to create a starting point.
Run into the post-obit diagram :
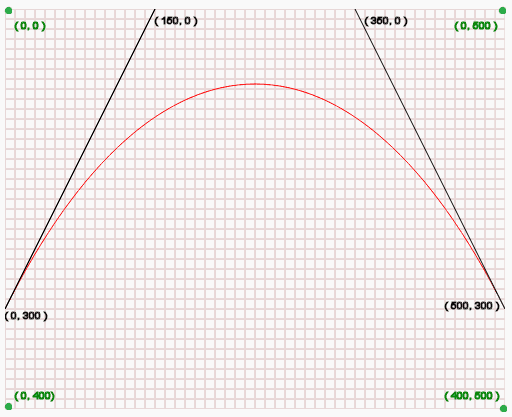
In the above diagram :
- (0, 0) is the tiptop-left position of the canvas.
- (0, 400) is the bottom-left position of the canvas.
- (0, 500) is the top-right position of the canvass.
- (400, 500) is the bottom-right position of the sheet.
- (0, 300) is the starting betoken of the curve.
- (150, 0) i.e. (cp1x, cp1y) is the first command position of the curve.
- (350, 0) i.eastward. (cp2x, cp2y) is the second command position of the curve.
- (500, 300) i.e. (x, y) is the ending signal of the bend.
Case : HTML5 Canvas Bezier Curve using bezierCurveTo() method
The following spider web document draws some directly lines and a Bézier bend (between two points) and creates the graphic symbol 'R'.
Output :

Code :
<!DOCTYPE html> <html> <caput> <championship>Sample arcs example</championship></caput> <body> <canvas id="DemoCanvas" width="500" top="400"></canvas> <script> var canvas = document.getElementById("DemoCanvas"); var ctx = canvas.getContext("2d"); ctx.lineWidth = 7; ctx.lineCap = "round"; ctx.clearRect(0, 0, canvass.width, canvas.height); ctx.beginPath(); ctx.moveTo(30, 200); ctx.lineTo(30, 50); ctx.lineTo(65, 50); ctx.moveTo(30, 120); ctx.lineTo(65, 120); ctx.lineTo(100, 200); ctx.strokeStyle = "black"; ctx.stroke(); ctx.beginPath(); ctx.moveTo(65, 50); ctx.bezierCurveTo(120, 50, 120, 120, 65, 120); ctx.strokeStyle = "light-green"; ctx.stroke(); </script> </body> </html> quadraticCurveTo() method
A quadratic Bézier curve requires two points. The first signal is a control point that is used in the quadratic Bézier calculation and the second point is the ending betoken for the bend.
Syntax :
quadraticCurveTo(cp1x, cp1y, 10, y);
| Parameters | Type | Description |
|---|---|---|
| cp1x | number | The x-coordinate of the Bézier control point. |
| cp1y | number | The y-coordinate of the Bézier command point. |
| x | number | The x-coordinate of the point to add together to the electric current path. |
| y | number | The y-coordinate of the bespeak to add to the current path. |
Note : The starting point for the curve is the concluding bespeak in the existing current subpath. If a path does not exist, employ beginPath() and moveTo() methods to fix a starting point.
Run across the following diagram :
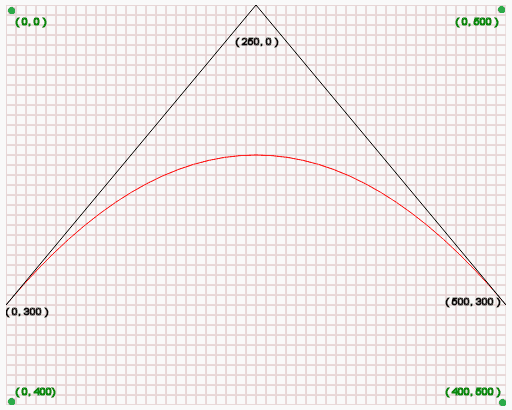
In the higher up diagram :
- (0, 0) is the top-left position of the sail.
- (0, 400) is the lesser-left position of the canvas.
- (0, 500) is the peak-right position of the canvas.
- (400, 500) is the bottom-right position of the canvas.
- (0, 300) is the starting betoken of the curve.
- (250, 0) i.e. (cp1x, cp1y) is the command position of the curve.
- (500, 300) i.e. (x, y) is the ending point of the curve.
Example : HTML5 Sail quadratic Bezier Curve using quadraticCurveTo() method
In this case, half-dozen shapes together create the following graphics.
Output :

Code :
<!DOCTYPE html> <html> <caput> <title>Sample arcs example</title></head> <body> <sail id="DemoCanvas" width="500" height="400"></canvas> <script> var canvas = certificate.getElementById('DemoCanvas'); if (sail.getContext) { var ctx = canvass.getContext('2d'); // Describe shapes ctx.beginPath(); ctx.moveTo(75,25); ctx.quadraticCurveTo(25,25,25,62.v); ctx.quadraticCurveTo(25,100,50,100); ctx.quadraticCurveTo(l,120,xxx,125); ctx.quadraticCurveTo(60,120,65,100); ctx.quadraticCurveTo(125,100,125,62.5); ctx.quadraticCurveTo(125,25,75,25); ctx.lineWidth = "3"; ctx.strokeStyle = "dark-green"; ctx.stroke(); } else { alert('Not supported in this browser.'); } </script> </torso> </html> See the Pen html css common editor by w3resource (@w3resource) on CodePen.
Previous: HTML5 Canvas Line
Next: HTML5 Sheet path tutorial
Source: https://www.w3resource.com/html5-canvas/html5-canvas-arc.php
0 Response to "Canvas Draw Circle at Radiu"
Postar um comentário